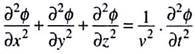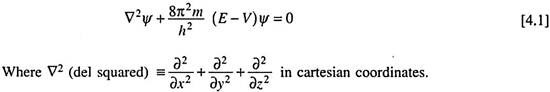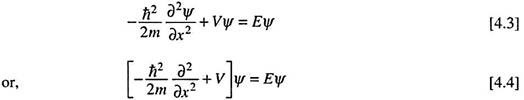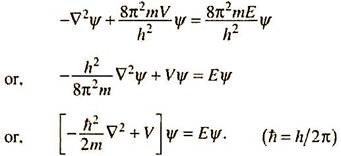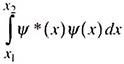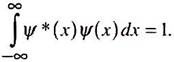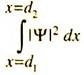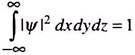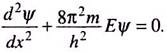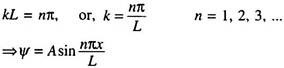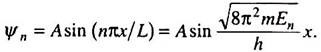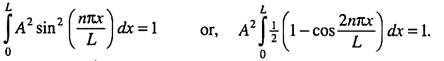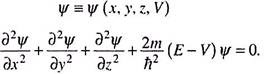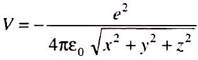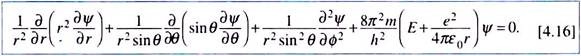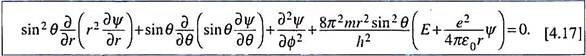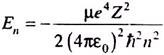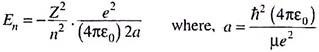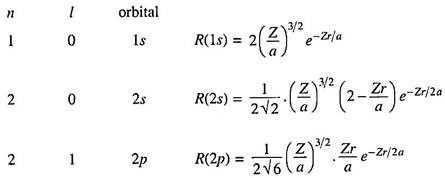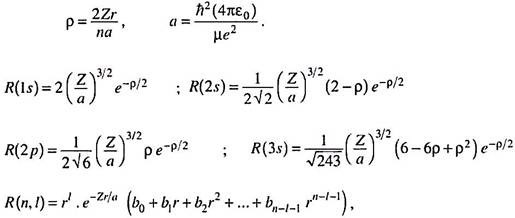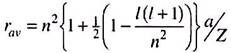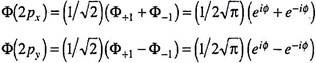Term Paper on Wave Mechanics | Atoms | Chemistry

In this term paper we will discuss about the wave mechanics.

The limitation of the Newtonian mechanics for atomic systems led to the development of a new approach suitable for systems with prominent wave character. Two independent developments appear significant in this connection – Heisenberg, Born and Jordan approached the problem with the properties of matrix (1925) while Schrodinger tried to develop a mechanics based on the properties of waves (1926).

Both approaches are called quantum mechanics because they developed around the central idea of quantization of energy (energy was supposed to be continuous in classical mechanics). Here we shall have a brief introduction to Schrodinger’s approach to quantum mechanics, popularly known as wave mechanics.

1. The Schrodinger Equation:

Classical Mechanics:

In classical mechanics, the state of a system is defined by specifying the forces acting on it and all the position coordinates and velocities (or momenta) of the constituent particles. The position and momentum of any particle at any instant of time may be stated precisely by equations derived from Newton’s laws of motion. But we cannot derive these laws of motion. We simply accept them and then apply them to a real observation. We recall the second law of Newton which summarily leads to ―

Force, F = mass x acceleration = m (d²x/dt²)

for a particle of mass m moving in the x-direction. This is a second order differential equation involving x, the position of the particle with respect to time t. If we know the force F and the mass m, we can find x by integrating the above equation twice. But this will introduce two integration constants. These constants may be evaluated by two pieces of information like the position and velocity of the particle at some given time, say at the beginning of the observation (t = 0). Thus we have our familiar relations like (in usual symbols) –

ν= u + ft

or, s = ut + ½ft² and so on.

These relations enable us to predict the precise position and momentum of the particle at any future time.

Such prediction of position and momentum with absolute precision is not possible for microscopic particles because of the inherent uncertainty of the system itself. We try to describe such systems through their associated matter waves. Before that, let us briefly summarize our understanding of wave motion.

Wave Motion:

Any common example of wave motion involves periodic variation of some property of the system; the property is thus a function of time. When we throw a small piece of stone in a tranquil pond, waves of water propagate in the form of concentric rings. The height of water (compared to the undisturbed level) at any point varies periodically with time. This displacement of any point in the wave (ɸ) may be expressed as a function of the space coordinates of the point and time t ―

ɸ ≡ f (x, y, z, t)

This description holds for any other wave motion. In electromagnetic waves, for example, the electric and magnetic fields vary periodically. The dependence of ɸ on the space coordinates and time is expressed by the relation ―

Where, ν is the velocity of the wave. If we restrict our attention to a wave propagating along the x-direction, we get the relation ―

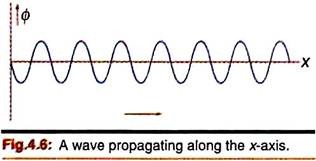
We may readily visualize such waves in a string attached at one end when a wave motion propagates along the x-direction. Such wave patterns (Fig. 4.6) are typical for simple harmonic motion and are expressed by sine or cosine functions,

ɸ = sin (kx — ωt)

Where, k = wave number = 2π/λ and ω = angular frequency = 2πν.

(λ, and ν are wavelength and frequency respectively.)

Matter Wave:

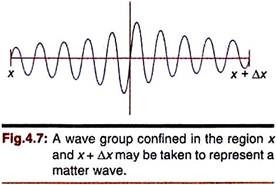
Now we want to describe a microscopic particle by its associated de Broglie waves. Clearly, such waves cannot be extended over a large span as shown in Fig. 4.7. We want that the wave will remain as close to the particle as possible. In other words, the wave function ɸ should be significant only around the actual position of the particle, say between x and x + Δx.

Such description in terms of waves involves wave groups formed by superposition of waves and represented by linear combination of several sine or cosine waves (Fig 4.7). The wave number k of the contributing simple harmonic waves will vary slightly from one another and so also will λ (= 2π/k).

An equation suitable for describing matter waves was arrived at by Schrodinger from the classical wave equation and de Broglie’s idea of matter waves but with the introduction of some new basic postulates. The equation cannot be derived from any more fundamental principles.

In this new approach, the state of a system is defined by a mathematical function Ψ (capital psi) which is a function of the space coordinates of the particles in the system and of time. For a single particle ―

Ψ = Ψ (x, y, z, t)

Where x, y and z are the space coordinates of the particle. The function Ψ may be real or imaginary and hence is abstract itself; but it can be related to measurable properties of the system and hence carries a meaningful significance to be discussed shortly.

If the total energy of a system remains unchanged with time, we may express Ψ as the product of two functions; one of the space coordinates (Ψ) and the other a function of time t.

Ψ (x, y, z, t) = Ψ (x, y, z). f (t)

The function Ψ (x, y, z) conforms to a wave which depends only on the space coordinates like a stationary wave created in a string bound at the two ends. The displacement of the string at any point may be obtained from solution of the general wave equation putting the appropriate boundary conditions.

We shall restrict ourselves to such time-independent wave functions and the corresponding time-independent form of Schrodinger equation. This is not unjustified. In an isolated atom or molecule, the potential energy V is independent of time and the system can exist in a stationary state of constant energy. In such cases we can apply the time-independent Schrodinger equation to obtain the allowed energy levels.

The time-independent Schrodinger equation, also called the steady state Schrodinger equation, is commonly written as ―

The equation is thus a second order differential equation involving a function Ψ. Ψ is called the wave function which is a function of the space coordinates of a point around which we intend to locate a particle of mass m, total energy E and potential energy V.

For a single particle (mass m) moving in the x-direction, the Schrodinger equation [4.1] gets the form ―

Substituting h/2 = ħ/ (h bar or h cross) equation 4.2 may be rearranged to get ―

The corresponding equation in three dimensions would be ―

If we replace the part in the square bracket in equations 4.4 or 4.5 by H, we get ―

HΨ = EΨ …[4.6]

H is an operator called the energy operator or Hamiltonian operator which, when operated on Ψ gives the energy E of the system.

All the equations from 4.1 to 4.6 are expressions of the Schrodinger equation (time- independent).

For collision between two molecules or for a molecule subjected to varying electric and magnetic fields of electromagnetic radiation, the condition of stationary state is no more applicable and one must deal with the time-dependent Schrodinger equation. In such cases, the wave function is obtained as ―

Ψ = Ψ.e^–iEt/ħ

The equation of Schrodinger based on matter-wave cannot be derived from any more fundamental principle. It has to be taken as the basic equation or postulate of quantum mechanics. The final form of the equation has to be appreciated from its agreement with experimental facts and not by its genesis.

A simplified approach to the construction of the equation is given below:

The Schrodinger Equation:

1. Wave Motion:

A simple example of wave motion in one dimension can be provided by a displacement moving along a string fixed at one end only. Suppose the string vibrates with a frequency ν, producing waves of length λ which travel in the positive x-direction with a velocity u. The amplitude y, i.e., the height of the wave at any point x and time t is a function of both x and t, that is, y = f(x, t).

Now, such a wave motion in one dimension can be represented mathematically by the general partial differential equation ―

(d²y)/ (dx²) = (1/u²) (d²y/dt²)

It can be shown by direct substitution that this equation is satisfied by any function of the form ―

y = f(x – ut)

For a wave travelling in the negative x-direction, the solution would be ―

y = g(x + ut)

Both f and g are arbitrary functions.

2. Standing Waves:

Vibration of a string fixed at its two ends produce standing waves or stationary waves. The length (l) of the string is now fixed, say between x = 0 and x = I. Any wave formed by the string will be guided by the condition that its amplitude must be zero at the two ends. This leads to the conclusion that all standing waves must satisfy the condition –

n x λ/2 = l, where n is an integer.

For any standing wave formed within the string, the function of x always has the same form irrespective of the value of t. The situation is analogous to a sine curve ― at certain values of x, there is a node in the wave at all times and at certain other values of x, the wave always has its maximum amplitude. (The magnitude of this maximum amplitude, however, oscillates with time). In this sense, a standing wave is an oscillatory motion; it is not strictly a wave motion as there is no propagation of energy along the string.

By actual application, it has been found that the equation representing a standing wave is most suitable to describe an electron wave in the atom. We may proceed to obtain the desired equation as ―

With separated variables, the amplitude y of the wave may be expressed as ―

y = f₁(x) f₂(t), where f₁(x) is a function only of x

and f₂(t) can be written as f₂(t) = A sin 2πνt …[4.8]

Here A is a constant equal to the maximum amplitude of the wave.

Therefore, y = f₁(x) A sin 2πνt

Differentiating y twice with respect to t at constant x, we get ―

dy/dt = f₁(x) 2ν A cos 2πνt

d²y/dt² = –4π²ν²f₁(x) A sin 2νt

From 4.8, d²y/dt² = – 4² ν²f₁(x) f₂ (t) …[4.9]

Therefore, from 4.7, d²y/dx² = – [(4π²ν²)/u² ]f₁ (x) f₂ (t) …[4.10]

Again, we differentiate y [= f₁ (x) f₂(t)] twice with respect to x at constant t ―

d²y/dx² = d²f₁ (x)/dx².f₂ (t).

Comparison with 4.10 now gives, d²f₁ (x)/dx² = – [(4π²ν²)/u²] f₁ (x) …[4.11]

The velocity of the wave, u is related to the frequency, ν, by the relation u = λ.ν, where λ is the corresponding wavelength. Hence, from 4.11 ―

d²f₁ (x)/dx² = – (4π²/λ²) f₁ (x) …[4.12]

This equation is applicable to a wave moving in one direction only. Extending this to a wave moving in three dimensions, f₁(x) is replaced by a new function depending on the three Cartesian coordinate’s ― Ψ(x, y, z). Writing simply Ψ for Ψ(x, y, z), equation 4.12 is transformed to ―

The symbol ߜ² (del squared) is often used to represent the differential operator (Laplacian operator); in cartesian coordinates,

3. Matter Waves:

The fundamental postulate of Schrodinger was that an equation of type 4.12 or 4.13 may be applied to all particles. The equations may be further adjusted by inserting the mass (m) and velocity (ν) of the particle concerned from the de Broglie relationship λ = h/mν. From 4.13 ―

The total energy E of the particle must be equal to the sum of its potential energy V and kinetic energy ½mv² ―

Substituting in equation 4.14, one gets, ߜ²Ψ + [8²m(E ―V)/h²] Ψ = 0

This is the wave equation of Schrodinger in the time-independent form (Eqn. 4.1).

We may rearrange the above equation to write ―

The part within square bracket may be represented by H to obtain Eqn. 4.6 ―

HΨ = EΨ

Where, H is called the energy operator or Hamiltonian operator.

Interpretation of Ψ:

How do we interpret the wave function Ψ? By this time we have seen that Ψ is a function of the space coordinates of the position of a particle of the system and is essentially the amplitude analogue of the associated matter wave. We may take the analogy of electromagnetic waves to get further insight into the nature of Ψ.

For electromagnetic waves, the intensity of radiation at any point is proportional to the square of the amplitude of the wave at that point. Again, the greater the intensity of radiation at a point, greater is the number of photons striking that point.

Combining these two relations, greater amplitude of electromagnetic waves at a point suggests a greater number of photons at that point. An alternative expression for this would be – the greater the amplitude of a light wave at a point, greater is the probability of a photon to be found there. The probability is thus related to the square of the amplitude.

Parallel arguments may be applied to a matter wave, e.g., the wave of an electron. Let the amplitude of this wave at a point (x, y, z) be Ψ. The probability of finding the electron near that point should be proportional to Ψ², the square of the amplitude function. As Ψ may also be complex, the probability is expressed by including its complex conjugate Ψ*.

Ψ*Ψ is real and represents the probability density, that is, probability per unit volume. The probability that an electron may be found in a small volume element dv will be given by Ψ* Ψdν. If a particle can move only along the x-axis and is characterized by the wave function Ψ(x), the probability density is Ψ*(x) Ψ(x). The probability that the particle may be located between x₁ and x₂ will be ―

The total probability of locating the particle between x = -∞ to x = +∞ must be unity, i.e.

Since the probability Ψ*(x) Ψ(x) dx is dimensionless, Ψ(x) should have the dimension of length^–1/2 or the unit m^–1/2. Wave functions in three dimensions will have the unit m^–3/2.

Max Born postulated (1926) that IΨI² gives the probability density of finding any particle at given locations in space at time t where Ψ is, as before, a function of the space coordinates of the particle and time t. Here IΨI is the absolute value of Ψ. If Ψ = a + ib, the absolute value of Ψ is defined as (a² + b²)^1/2. Also,

Ψ* = a – ib and Ψ*Ψ = (a – ib) (a + ib) = a² + b² = IΨI²

For a one-particle, one-dimensional system, the probability of finding the particle in the region d₁ to d₂ is given by ―

For stationary states, we have similar expressions using the space-only function Ψ.

In fact, the implications of the wave function are not limited to position only. The function provides information on the outcome of a measurement of any property of the system, position, momentum, energy, angular momentum etc.

Finally, the wave function is not to be associated with any physical wave. It is an abstract mathematical entity though it provides information on physical quantities which may be verified experimentally.

The Schrodinger equation thus specifies the laws of motion relevant to particles of microscopic systems. The theory includes Newtonian mechanics as a special case.

Some of the properties of the wave functions are as follows:

1. Eigenfunctions and Eigenvalues:

We recall the form of the time-independent Schrodinger equations 4.5 or 4.6 ―

We mentioned the part in the square bracket as the Hamiltonian operator H (also written Ĥ) or the energy operator, since it yields the energy E of the system when applied on Ψ. Here H operates on Ψ to give E times Ψ. In general when an operator  (a hat, to indicate that A is an operator) operates on a function Ψ_i to give back the function multiplied by some constant a_i, that is,

ÂΨ = a_iΨ_i

Operator (function) = constant x same function

We say that Ψ_i is an eigenfunction of the operator  and a_i is its eigenvalue (eigen ≡ appropriate). In case of the Hamiltonian operator H mentioned above, Ψ(x) is an eigenfunction and the several values of E that are obtained for various wave functions are eigenvalues.

(d/dx) of e^kx is k.e^kx. Hence e^kx is an eigenfunction of (d/dx) with an eigenvalue k.

2. Well-Behaved Wave Functions:

The Schrodinger equation in its steady-state or time-independent form may have more than one solution for Ψ. But all of them may not correspond to physical reality. We want only those solutions of the Schrodinger equation which will give us information on physically measurable properties of the system (though Ψ itself is an abstract entity). Thus an acceptable wave function or well-behaved wave function should not only satisfy the Schrodinger equation, but also obey certain conditions pertinent to the system.

Such acceptable solutions for the wave function (eigen functions) are selected according to the following conditions:

Condition 1:

Ψ must be single-valued. This means Ψ may have one and only one value at any point in space. This is necessary to ensure that the corresponding probability at any point may have only one value.

Condition 2:

Ψ must be finite. The probability density at any point in space must be finite— an infinite probability density at any point signifies that the particle is present precisely at that point only. Accordingly Ψ should vanish at infinity.

Condition 3:

Ψ must be continuous. Certain properties like the momentum are calculated by taking the derivative of Ψ. If Ψ is discontinuous at some point, its first derivative at that point will be infinite. But values of physical properties cannot be infinite.

Condition 4:

If Ψ must be square integrable. This allows multiplication of Ψ by a constant to make it normalized; this means the total probability of finding a particle described by Ψ over entire space must equal unity ―

If Ψ is a solution of the Schrodinger equation, so also is kΨ, where k = constant. This is called the normalization constant.

We shall learn the implications of these conditions further in connection with the particle in a box problem.

2. Particle in a Box:

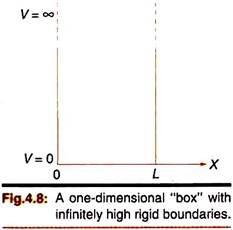
The simplest illustration of the application of Schrodinger equation is provided by the particle in a one-dimensional box problem. Let us consider a particle trapped in a region of space in one-dimension (along the x-axis, say); it is restricted to move between x = 0 and x = L by infinitely high impenetrable walls. The situation is analogous to a particle confined in a box or a square well (one-dimensional) whose walls are infinitely high [Fig. 4.8].

The particle does not lose energy when it collides with such walls; hence its total energy remains constant. The potential energy V of the particle within the box is also constant—for convenience we assume it to be zero. On both sides of the box, the potential is infinite. We assume that the behavior of the particle in the box can be described by the Schrodinger wave equation (time-independent form). Since the energy of the particle is finite, it cannot exist outside the box, that is in regions with x < 0 and x > L. So the wave function of the particle, Ψ, is zero in these regions.

Inside the box, V = 0; the Schrodinger equation (Equation 4.2) becomes ―

The differential equation may be written as ―

The general solution of this differential equation is ―

Ψ = A sin kx + B cos kx.

Boundary Conditions:

At x = 0, and at x = L, Ψ must be zero.

0 = A sin (0) + B cos (0) or B = 0.

The equation thus reduces to Ψ = A sin kx.

At the other wall, i.e., x = L, Ψ = 0; Hence, 0 = A sin kL.

A cannot be zero since then Ψ itself vanishes (trivial solution); so we have sin kL = 0.

This occurs when ―

From the value of k², we get ―

We see at once that the energy has been quantized in terms of the integral values of n. The particle can now assume only discrete energy values E_n corresponding to each integral value of n. These are the energy eigenvalues corresponding to the Eigen functions ―

Here n quantizes the energy; so it becomes a quantum number.

These Eigen functions satisfy the conditions for a well-behaved function. For each value of the quantum number n, Ψ_n has a definite value at any point x. – it is thus single-valued. Ψ_n and ∂Ψ_n/∂x are both continuous.

For normalization, we note that the particle is confined within the region x = 0 to x = L and hence the total probability of finding the particle in this region must equal unity ―

Simplifying, we get A = √(2/L). The normalized wave functions of the particle are therefore—

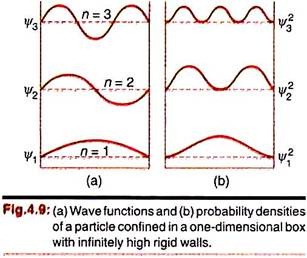
The nature of plot of the wave functions for n = 1, 2 and 3 and the corresponding probability densities, lΨ₁l², lΨ₂l², are shown in Fig. 4.9. We observe that Ψ_n may be both positive or negative, but |Ψ_n|² is always positive.

The classical momentum p_x of the particle corresponding to the energy value E_n(= p _x²/2m) gives ―

p_x = + (nh)/(2L); n = 1, 2, 3, …

From the de Broglie relation, λ = h/p_x,

λ = [h/ (nh/2L)] = 2L/n i.e., L = nλ/2.

Thus for each Ψ_n, the length of the box should contain an integral number of half-wavelengths, as seen in Fig 4.9(a). The waves thus resemble the possible modes of vibration of a stretched string.

The plots of the probability densities are also interesting (Fig 4.9(b)). For n = 1, the most probable position of the particle is at L/2; but for x = 2, this point corresponds to a node, i.e., the probability of finding the particle at the point becomes zero. For every Ψ_n, there are n – 1 number of nodes (in addition to those at the boundaries).

The particle has high probability of being found on either side of these inner nodes. This necessitates a change in our classical outlook for the “particle” when it is subjected to wave mechanical treatment –the “particle” cannot simply “roll” along the x-axis showing maxima at some point and nodes at some other points.

Classically, the particle can roll back and forth within the walls—the probability of finding it anywhere between x = 0 and x = L is constant. The classical probability function has a value of 1/L. The quantum mechanical treatment shows n number of peaks of probability where n is the quantum number. As n becomes very large, the number of peaks increases and the separation between them decreases. Ultimately they will merge and the situation will become identical to the classical description. There is thus correspondence between the classical and the wave mechanical descrip­tions.

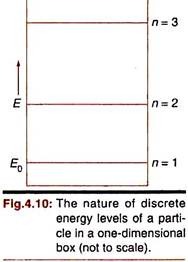
The same correspondence is revealed when we consider the energy of the particle (Fig. 4.10). Classically a particle inside the one-dimensional box may have any positive energy. But our wave-mechanical treatment spontaneously leads to discrete quantized energy levels (E_n = n²h²/8mL²; n = 1, 2, 3,…). Since n cannot be zero (in that case the whole wave-function will disappear), the particle in the box has a minimum energy of (h²/8mL²) (= E₀) even at absolute zero—its residual energy or zero-point energy.

The occurrence of definite energy levels for the particle does not contradict the uncertainty principle – ΔEΔt > h. The wave functions in this case represent stationary states for which time is unspecified, that is Δt is infinite. Hence ΔE will be zero.

The energy of the particle depends directly on n². As n increases, the successive energy levels get closer and closer and ultimately they merge into a continuum. This shows correspon­dence between micro and macro descriptions of a system.

From equation 4.15, we can also follow the dependence of energy of the particle on the mass (m) of the particle and length (L) of the box. The energy of the particle depends inversely on m and L². Hence a particle with the mass of an electron in a linear region of the order of a molecule will have much wider separation between the energy levels than a molecule in a one-dimensional box of few centimeter lengths. The same reasoning will apply to a cubic box. In fact the energy levels of thermal motions of molecules (in three dimensions) are so close that their kinetic energy appears to vary continuously.

Let us express the energy of the particle for n = 1 state by E₀.

Then, E₀ = (h²/8mL²); E_n = n²E₀.

∴ E_n+1 – E_n = [(n + 1)² – n²] E_n = (2n + 1)E₀

For a particle of m = 1 g (0.001 kg) in a box of length 10 cm(0.1 m), with a velocity 10 cm s^–1,

E₀ = (h²/8mL²) = 5.5x 10^–63 J; kinetic energy (½mv²) = 5 x 10^–6 J.

The quantum number n corresponding to this energy would be given by ―

n² = E_n/E₀ = 5 x 10^–6 / 5.5 x 10^–63 ≃ 10⁵⁷ Þ n ≃ 3 x 10²⁸.

The spacing between the energy levels in this high quantum number range will be so small (~10^–35 J) that they will appear continuous. Here again we see the correspondence between macro and micro systems.

For a two and a three-dimensional box, the wave function would separate into two and three equations respectively, each having the same type as the one for one-dimensional box. The allowed energies may then be expressed as (L = side of the box) ―

Two – dimensional box – E = (h²/8mL²)(n_x² + n_y²)

Three – dimensional box – E = (h²/8mL²)(n_x² + n_y² + n_z²).

3. The Hydrogen Atom:

The hydrogen atom consists of a central proton (charge +e) and an extra-nuclear electron (charge –e). Since the mass of a proton is nearly 1836 times the mass of an electron, one may consider the proton to be stationary while the electron moves around it under a balance of electric and mechanical forces. As shown in connection with Bohr’s theory, the motion of the proton may be adjusted by replacing the mass m of the electron by its reduced mass µ (= 0.999456 m).

To begin with, we have the time-independent Schrodinger equation (for stationary states of the atom) with the wave function of the electron Ψ which is a function of the space coordinates x, y, z and the potential energy V ―

E is the total energy of the electron; the potential energy V of the electron at a distance r from the nucleus is –

Since V is a function of r, we cannot substitute it directly in the Schrodinger equation written above using cartesian coordinates. The situation may be tackled by writing ―

An alternative, and also a more realistic approach in view of the spherical symmetry of the system, would be to express the Schrodinger equation using spherical polar coordinates. For this, we have to understand the interrelation between the cartesian and polar systems of coordinates and the corresponding modification of the Laplacian operator ߜ².

The Schrodinger Equation in Polar Coordinates:

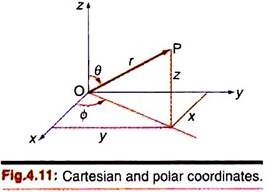
The interrelation between the Cartesian and spherical polar coordinates of a point (P) may be understood with reference to Fig. 4.11.

ɸ = azimuth angle = angle between the projection of the radius vector on the xy plane and the +x axis = tan^–1 (y/x).

r = length of radius vector from origin O to point P

θ = zenith angle (angle between radius vector and +z axis).

The coordinates x, y, z and r, θ, ɸ for the point P in the two systems (origin at the nucleus O of the atom) are related as ―

x = r sinθ cosɸ; y = r sinθ sinɸ; z = r cosθ and r² = x² + y² + z²

Accordingly, the Laplacian operator ߜ² becomes –

Using this expression for ߜ² and putting V = –e²/4ԑ₀r, the Schrodinger equation for a one electron system like the hydrogen atom has the form ―

E is the total energy of the electron; its mass m should be actually replaced by the reduced mass µ. For other hydrogen-like species the potential energy will be –Ze²/4ԑ₀r. The equation may also be expressed in the following form by r²sin²θ ―

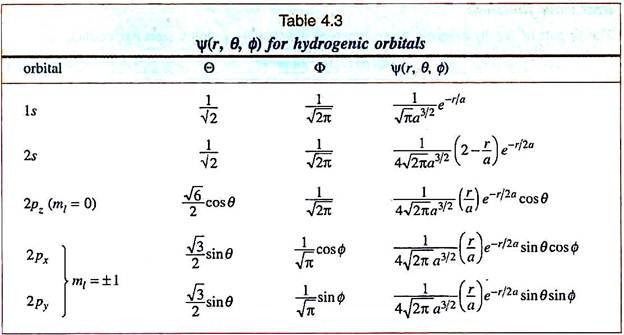
The Schrodinger equation in the polar form has an advantage – one can express Ψ as a product of three functions Ψ_r (or R(r)), (or Θ (θ)) and Ψ_ɸ (or Ф (ɸ)) which depend only on r, θ and ɸ respectively –

Ψ (r, θ, ɸ) = Ψ (r) Ψ (θ) Ψ (ɸ) = R (r) Θ (θ) Ф (ɸ) …[4.18]

R(r) or Ψ_r is a function of r, the radial distance from the nucleus. This is therefore called the radial part of the wave function, or simply the radial function and abbreviated by R. Ψ (θ) or Θ(θ) is a function of θ and Ψ(ɸ) or Θ(ɸ) is a function of ɸ. The last two functions represent the angular part of the wave function. They may also be combined into a single function Ψ (θ, ɸ) ―

Ψ (r, θ, ɸ) = Ψ (r) Ψ (θ, ɸ) …[4.19]

Solution of equation 4.18 leads to three quantum numbers to describe the electron in a hydrogen atom. In Bohr’s treatment only one such quantum number (n) was introduced. Similarly, the state of a particle in a one-dimensional box also introduced one quantum number. The motion of the electron considered in a three-dimensional space now introduces three quantum numbers for meaningful and well-behaved solution of the Schrodinger equation. They have the same set of values as assigned before from spectroscopic studies.

These are:

(i) The Principal quantum number (n) = 1, 2, 3 …

(ii) The Orbital quantum number (l) = 0, 1, 2 … (n – 1)

(iii) The Magnetic quantum number (m_l or m) = 0, ± 1, ± 2 … ± I.

A fourth quantum number (spin) was introduced later. For a given energy state, the radial function R depends on the values of n and l. This is often expressed by writing n and I as subscripts, i.e., as R_nl. Similarly, the Θ-function depends on I and m while Ф depends on m only. Summarily, the hydrogen-like wave functions are written as ―

Ψ = R_nl (r) Θ_lm (θ) Ф_m (ɸ) …[4.20]

These well-behaved one-electron spatial wave functions (obtained as solutions of the Schrodinger equation with one-electron Hamiltonian) for hydrogen and hydrogen-like species are called orbitals (Mulliken). The state of an electron in the atom is described by a characteristic wave function or orbital, designated by appropriate n and l values when we say that the electron “occupies” the orbital.

These orbitals are conveniently expressed by the numerical values of n and certain letters (s, p …) for the l values:

Thus an 1s orbital means a state represented by a wave function having n = 1 and l = 0.

Since a hydrogen-like atom has only one electron, all the hydrogen-like wave functions are orbitals. For many electron atoms we may find an approximate one-electron wave function by subjecting an electron to a combined field of the nucleus and all other remaining electrons.

Energy of the Electron:

Solutions of the R(r) or radial part of the wave equation for the hydrogen (and hydrogen-like) atom must satisfy the physical condition that R(r) should vanish as r → ∞. This leads to discrete energy values of the system depending upon n, the principal quantum number ―

The energy is negative and has the same expression as derived before. It may also be expressed as ―

Substitution gives a = 0.5295Å (against 0.5292Å for a₀, the first Bohr radius. Clearly, a ≃ a₀ when µ = m (for a supposedly infinite mass of the nucleus).

The ground state energy for hydrogen may be calculated by putting Z = 1 and n = 1 in the above expression of E_n when we get ―

E = – 2.179 x 10^–18 J = – 2.179 aJ (a for atto, 10^–18)

= –13.60 eV

The ionization energy of a hydrogen atom would be accordingly 13.60 eV.

The energy for other values of n and Z in different hydrogen-like species (He⁺, Li²⁺ etc.) may be found by the generalized formula ―

E_n = – (Z²/n²) x 13.60 eV.

Here we have ignored the variation in µ owing to change in mass of the nucleus.

Atomic Units:

In quantum chemistry, some conventional non-SI units are found for length and energy. The first Bohr radius of hydrogen (a₀) is taken as the atomic unit of length and called 1 bohr.

1 bohr = a₀ = ħ² (4ԑ₀)/me² = 0.5292 Å.

The potential energy of two electrons separated by the Bohr radius is called the Hartree energy (E_h) which is the atomic unit of energy.

1 Hartree (E_h) = e²/(4ԑ₀)a₀ = 27.211 eV

Or, 4.3598 x 10^–18 J.

If we approximate a by a₀, the energy of the hydrogen atom (ground state) is – ½ hartree. This value is also used as a unit in many cases, called a rydberg (Ry).

1 rydberg = E_h/2 = 2.18 x 10^–18 J.

Radial Wave Function, R_nl:

The radial part of the wave function (R_ml or simply R) depends only on n and l and is independent of θ and ɸ. Some typical examples of hydrogenic radial wave functions are –

Radial functions are also expressed conveniently in terms of the dimensionless quantity r―

Where b₀, b₁ … are constants whose values depend on n and l.

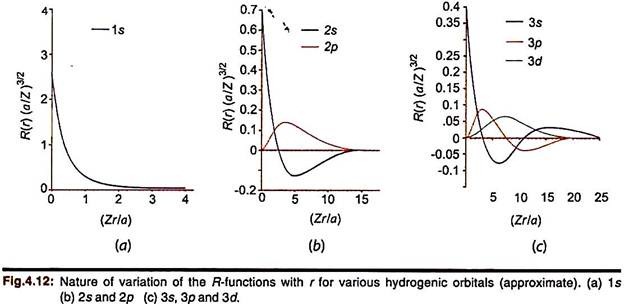
The important general features of these functions are understood better from their plot against the radial distance r. For convenience, the functions may be multiplied by some suitable factor in the plot. Fig.4. 12a-c shows some typical plots of R(r) (a/Z)^3/2 vs (Zr/a) for some hydrogenic orbitals.

Some important general features of radial functions:

(i) All the functions contain an exponential term which decreases with r (“decays”) as exp (–Zr/na). So R (2s) has a slower rate of decay with r than R(1s). Thus the wave function of an orbital with higher n extends to a larger distance from the nucleus.

(ii) The R-function for the 2s orbital passes through zero when (2 – Zr/a) = 0, i.e., at r = 2a/Z, R (2s) = 0. The point at r = 2a/Z thus represents a radial node. The function changes its sign beyond this point. It can be shown that an orbital designated by n and l has n-l-1 number of radial nodes (the node at the origin is not counted).

A node is a surface where the wave function passes through zero as it changes sign, as at r = 2a for the 2s orbital in hydrogen atom. This is an example of a radial node or spherical node as the radial function passes through zero over a spherical surface at this distance from the nucleus. The numbers of such spherical nodal surfaces arising from a radial function are (n-l-1), as shown below ―

Besides such radial nodes, there are also angular nodes.

Radial Distribution Function:

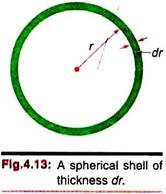
In wave mechanical interpretation the probability of finding a particle at some point is propor­tional to the square of its wave function Ψ for that point. So the dependence of probability on the radial distance from the nucleus will be obtained from the square of the radial part of the wave function, Ψ(r)² or R². We may consider the atom to be composed of concentric layers of thin shells of thickness dr and calculate the volume dν of such a shell between r and r + dr ―

V = 4πr³/3

dV = 4πr²dr.

The probability that an electron will be found in this volume is R²dV or 4r²R²dr. The function 4R²r² or more generally (for non-spherical orbitals) is called the radial distribution function, P(r). When multiplied by dr, the function gives the probability of finding the electron anywhere in the shell of thickness dr at a distance r from the nucleus. In this sense P(r) may be considered the radial probability density.

For the 1s orbital of hydrogen, (Z = 1), we may write, from ―

So the radial distribution function P(r) will be ―

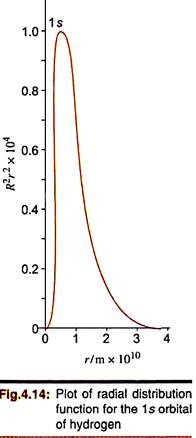
Fig. 4.14 shows the nature of plot of P(r) vs r.

From the above figure we can observe the following:

(i) The radial distribution function R²r² is zero at the nucleus because of the r² term, since, r = 0 at this point.

In contrast, the R-function had a very high value at r = 0.

(ii) Whereas the R-function decreases exponentially but r² increases rapidly with r, the resultant plot of R²r² passes through a maximum at an intermediate value of r. This is called the most probable radius, r_mp. For hydrogen, this occurs at 53 pm (0.53 Å) which is the radius of the first Bohr orbit. This also represents the most probable distance (r_max) which decreases with nuclear charge in hydrogen-like ions ― r_max = a/Z. The exponential term in the R function, exp (–Zr/na), also suggests that R²r² will decrease less slowly as n increases. Accordingly, r_max increases as n increases.

(iii) Owing to the presence of the exponential term, P(r) → 0 as r → ∞.

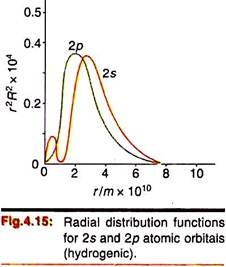
Radial distribution functions for orbitals higher than 1s may be similarly plotted against r (Fig. 4.15). These curves also show nodes corresponding to the nodes in their radial function (R). But the radial distribution function is always positive and shows one or more maxima. Thus the 2s orbital shows a first maxima at 0.8a (0.04 nm) followed by a node (at 2a) and finally a second outer maxima at 5.2a (0.28 nm). This shows that the 2s orbital has actually two concentric lobes separated by a nodal surface.

The distribution functions decay exponentially according to exp [–(Z²r²)/(n²a²)]. The negative sign with n² in the denominator suggests that the probability maxima will shift to right as n increases. Also, the rate of decrease will be slower as n increases. One can also calculate the mean radius of an orbital which is the expectation value of r calculated as –

The 1s atomic orbital in a hydrogen atom has a mean radius equal to 3a/2 or 0.79 A°. For other hydrogen-like species in their ground-state, árñ = 3a/2Z.

For an orbital with quantum numbers n and l, the mean radius is given by the general expression ―

For a given value of n, the mean radius decreases as l increases. Thus, the 2p orbital (l = 1) has a smaller mean radius than the 2s orbital (l = 0).

Penetration:

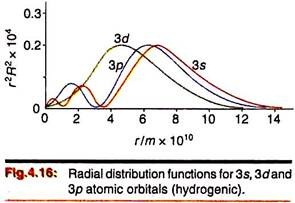
The radial distribution func­tions of the 2s, 2p, 3s etc. orbitals show small but finite presence within the inner orbitals. Comparison of Figures 4.14—4.16 reveals that the radial density of the 2s orbital spreads into the curve for the 1s orbital; the 3s orbital spreads into the 2s and 1s orbitals and so on. This is termed “penetration” of orbitals—that is, their distribution into inner electron cores.

As a consequence of penetration, an electron in an outer orbital does not get the full screening by the inner electrons from the nuclear charge. If the radial distribution of the 2s orbital had been distributed completely “outside” the 1s orbital, the 2s electron(s) would be completely screened by the 1s electrons. Since the 2s orbital penetrates somewhat into the core of 1s electrons, the screening will be less. The extent of penetration decreases from s to f orbitals ―

s > p > d > f.

This variation in penetration influences mutual screening of the electrons and hence controls the effective nuclear charge as well as the relative energy of the orbitals. The consequences are far-reaching, as we shall encounter in connection with ionization potential, electronegativity, size, oxidation state etc.

The radial distribution functions shown above are for Z = 1. Enhanced nuclear charge does not change the gross shapes of the curves, but their extension into space is reduced. This is called contraction of the orbitals. Such contraction is determined by several other factors, particularly the presence of other electrons in the system.

Angular Parts of the Wave Function:

The angular parts of hydrogenic wave functions (equation 4.18) are of the type shown in Table 4.1. As we shall soon appreciate, it is useful to consider them together as the product function Θ (θ) Ф (ɸ) (abbreviated ΘФ).

If we attempt to plot the ΘФ function against the independent variables θ and ɸ, we shall require a three-dimensional coordinate system ― one for θ, one for ɸ and the other for the dependent variable ΘФ. θ ranges from 0 to and ɸ ranges from 0 to 2 (Fig. 4.11). We may even use a cartesian coordinate system and choose to plot θ along the x-axis, ɸ along the y-axis and ΘФ along the z-direction. The ΘФ values will now describe a surface. At any point (θɸ), the height of the surface from the xy plane will give the corresponding value of ΘФ. The angular part of the probability density in the direction θɸ will now be given by Θ²Ф².

Spherical polar coordinates are more suitable for understanding the variation of ΘФ (or Θ²Ф²) with θ and ɸ. Conventionally, the function is plotted along the r-coordinate, measured from the origin (supposed to be at the nucleus of the atom). θ and ɸ are plotted along their respective coordinates. The plot, the locus of the points corresponding to ΘФ (or their square) now describes a characteristic surface for each type of orbital. The shape of the surface tells us about the nature of variation of the angular function (or the angular probability density) with direction.

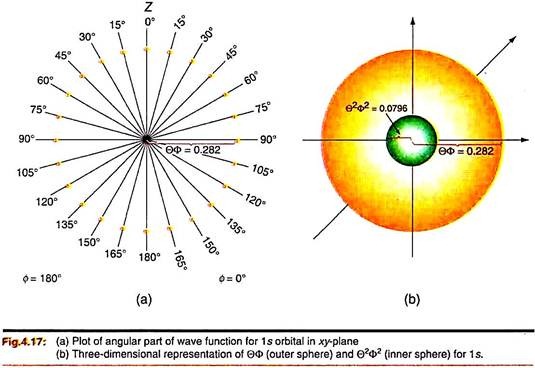
As an example, we first consider the 1s orbital (hydrogenic). From Table 4.1, ΘФ for this wave function is independent of θ or ɸ and is equal to 1/√4 (= 0.282). So the function ΘФ will have the same value for the full range of θ (0 – ) and ɸ (0 – 2). Before we appreciate the nature of the three dimensional plot, we begin with a two-dimensional plot of ΘФ on the xz-plane. What we simply do is that we draw radial lines from the z-axis (θ = 0°) at regular small intervals, say 15° upto θ = 180°.

We mark the distance 0.282 from the origin on these lines (any unit). We shall find that the dots (or their locus) form a semicircle (Fig. 4.17a) covering θ = 0 – 180° and ɸ = 0°. If we continue plotting similar dots on the θ = 180° half-plane, we get a circle. Since the value of ΘФ is independent of θ and ɸ, the plot will look the same on any vertical plane containing the z-axis. So we can mentally get the 3-dimensional plot of the ΘФ function by rotating the circle about the z-axis.

We actually get the cross-section of a sphere of radius 0.282 (Fig. 4.17b). Similarly we can get the plot of Θ²Ф² as a sphere of radius (0.282)² (= 0.0796) (Fig.4.17b; green core). Since the values of ΘФ and hence Θ²Ф² do not change with direction, the angular probability density will be same in all directions. We say that the 1s orbital is spherically symmetrical.

Similar plots may be done for the angular part ΘФ or its square for other orbitals. The procedures for p_z and p_x orbitals are illustrated in the box.

Angular Functions of 2p-Orbitals:

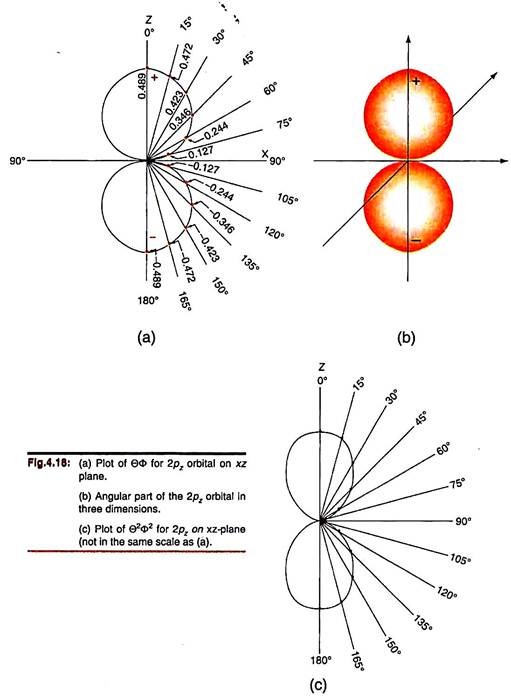
2p_z-Orbital:

We begin with the 2p_z-orbital as its angular function depends only on θ (√3/471 cosθ; Table 4.1). So for a given value of θ, the function ΘФ will have the same value on any plane containing the z-axis. We choose to plot the function on the xz-plane and draw radial lines from the origin at intervals of 15° for θ (Fig. 4.18). Now we mark the values of ΘФ for different θ on these lines (Table 4.2).

We find that the points for ΘФ fall on a semicircle between θ = 0°– 90°, the function becoming zero at θ = 90°. The points between θ = 90° to 180° repeat a similar semicircle; here the values of the function are all negative.

As the function is independent of ɸ, we expect a similar semicircle on the left half-plane. Thus we have two circles touching one another at θ = 90°. The circumference of one circle describes positive values of the angular function while in the other, the circumference covers negative values of the function. Since the angular function is independent of ɸ, it will have the same value on all vertical planes passing through the z-axis. So, we can get the three-dimensional description of the angular function by rotating these circles along the z-axis. We get two hollow spheres touching one another at the origin.

The surfaces of these spheres convey the angular variation of the ΘФ function. Any straight line drawn through the origin at any direction will touch the surfaces of these two spheres at two opposite points which give us the values of the angular function in that direction. There is no information inside the spheres as such.

Instead of ΘФ, one may also plot Θ²Ф² for the 2p_z-orbital (4.18c). In this case the values (squares) are all positive and it is redundant to write ‘±’ sign on the lobes.

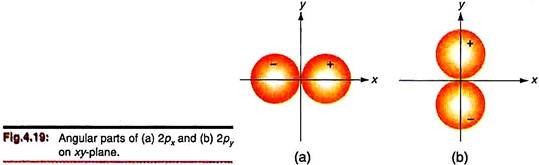
The 2p_x (and 2p_y) Orbitals:

Angular functions for p_x and p_y orbitals may be similarly plotted. However, the two angular functions are different and we need separate treatment for each. The function for p_x orbital (√(3/4π) sinθ cosɸ) depends on both θ and ɸ. Since cos ɸ = 0 at ɸ =  π/2 or 3/2, the angular function becomes zero at all points on the yz-plane. This provides a nodal plane. The p_x angular function is advantageously plotted on the xy-plane for which θ = /2.

Since sin /2 = 1, the angular function becomes √(3/4) cosɸ. We recall that the range of ɸ is 0° – 360° and draw radial lines along directions of ɸ varying by 15°. The values of the ΘФ function (calculated for each ɸ) are now marked on these lines. Again we get two spheres in three dimensions as in the case of the p_z orbital but these spheres have their centres along the x-axis (Fig. 4.19).

Angular function for the p_y orbital may be similarly plotted on the xy plane.

Angular nodes result when the angular function (ΘФ) becomes equal to zero and are planar or conical. There are l angular nodes in any orbital. The d_z2 orbital has two conical surfaces meeting at the nucleus and passing between the two sets of lobes; this is counted as 2.

The numbers of angular nodes for s- p- and d- orbitals are as follows:

s-orbital – 0

p-orbitals: 1 plane for each

d-orbitals – 2 planes for each, the conical surface in d_z2 being counted as 2.

An orbital has a total of (n – 1) nodes – (n – l – 1) radial nodes and I angular nodes.

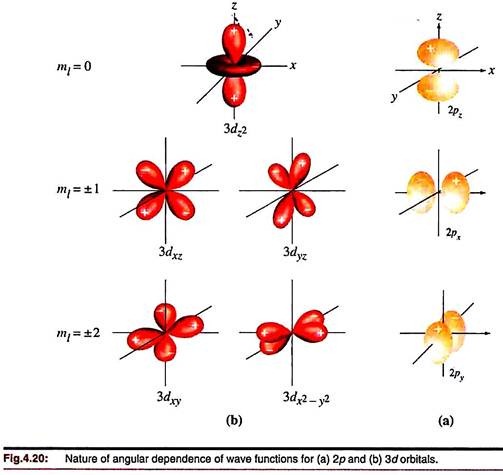
d-orbitals:

There are a set of five d-orbitals (Fig. 4.20) labeled according to their orientation in a cartesian frame. The d_xy, d_yz and d_zx have their symmetry axes lying on the respective planes but pointing between the concerned axes. The symmetry axes of the d_{x2 – y2} orbital lie in the xy plane with its lobes along the x and y-axis. Two analogous wave functions can be written for the other two pairs of axes, lebeled as d_{y2 – z2} and d_{z2 – x2}. But there are only five independent solutions of the wave equation corresponding to the d type (l= 2), i.e., only five nd orbitals are physically enough.

The three solutions of the type d_xy are independent of each other, but the three solutions of the type d_{x2 – y2} are not. By convention, the d_{y2 – z2} and d_{z2 – x2} functions are combined to give a single solution labeled as d_z2. This function corresponds to two main lobes directed along the z-axis and a collar perpendicular to the z-axis and symmetrical about the xy plane. Now d_xy, d_zx, d_yz, d_{x2 – y2} and d_z2 describe five independent d-orbitals.

Each has two nodal planes passing through the nucleus.

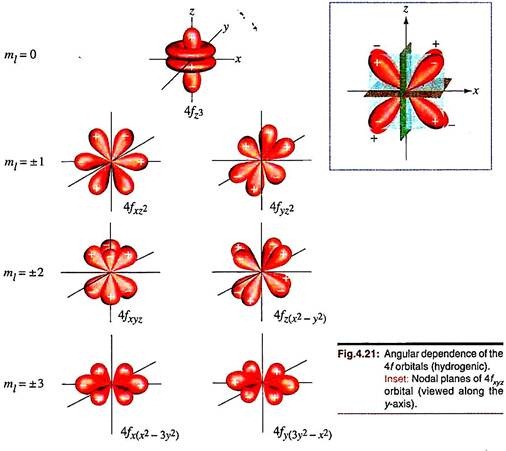
The f-orbitals have angular functions corresponding to six lobes and three nodes passing through the nucleus. Seven such orbitals are physically meaningful (Fig. 4.21).

Angular Probability Function:

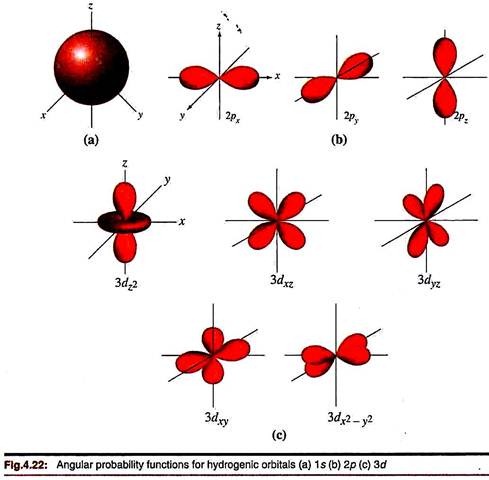
The probability of finding an electron in a given direction, summed over all distances from the nucleus, is proportional to the square of the angular functions. Θ²Ф² is thus called the angular probability function. For an s-orbital, the spherical symmetry remains unchanged on squaring. But the sign of the wave function is obviously dropped since the probability is always positive (Fig. 4.22). For p orbitals, the envelope becomes more elongated (Fig. 4.22b); the ‘+’ and ‘-‘ signs necessarily disappear. Similar changes occur for the d and f orbitals.

Total Wave Function (Space-Part):

The total wave function (time-independent) for any hydrogenic orbital is obtained by combining the radial and angular functions as –

Ψ (r,θ, ɸ) = R(r)Θ(θ)Ф(ɸ)

Some examples for the hydrogen atom (Z = 1) are given in Table 4.3.

Real Wave Functions:

The Ф part of the hydrogenic wave function is actually complex―

Where, m (or m_l) is the magnetic quantum number. Because it is convenient to work with real functions, we can convert them to real functions with the help of another theorem in quantum mechanics ―

Any linear combination of two or more stationary-state wave functions belonging to the same degenerate energy level will be an eigenfunction of the Hamiltonian operator with the same energy value. For example, the 2p orbitals have m_l = 0, ±1. Conventionally m_l = 0 refers to the z-axis taken as reference; hence Ф (2p_z) is simply 1/√(2). For p-orbitals with m_l = ±1, we take the sum and difference of the two Ф functions ―

Since e^+iɸ = cosɸ ± i sinɸ, we get ―

To get the real wave function for Ф (2p_y), we divide it further by i to get Ф (2p_y) = (1/√) sinɸ.

Similar linear combinations are used to obtain real wave functions for higher states of the H-atom.

Representation of Orbitals:

Orbitals are mathematical functions, real or complex. There are several ways for their representation which help us in understanding the directional character of bonds formed by atoms. Each representation is partial but useful in different contexts.

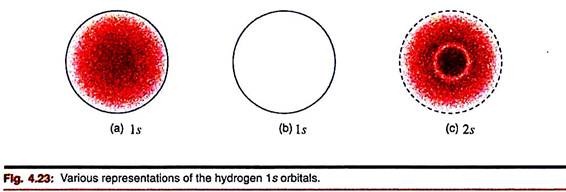
The most popular way of representation of orbitals is based on the idea of probability density through plot of Ψ². The electron dot representation is very common in this respect— the greater the density of dots at a region, the greater is the probability of an electron to be found there. For ready reference, we often imagine a sphere which contains most of the probability density, say 90 or 99 per cent, and take this as the limiting size of the orbital (Fig. 4.23a).

Sometimes only the boundary line (a circle in two dimensions) is retained (Fig. 4.23b). For higher s orbitals, this representation corresponds to the outermost maxima in the radial density curve. There will be radial nodes as one passes inward to the nucleus (Fig. 4.23c).

It can be shown that for the 1s orbital in an atom of hydrogen, the region for 90 per cent probability is a sphere of radius 1.40 Å.

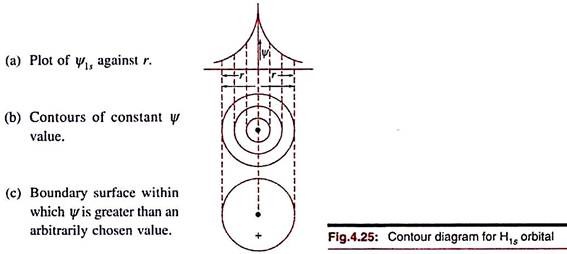
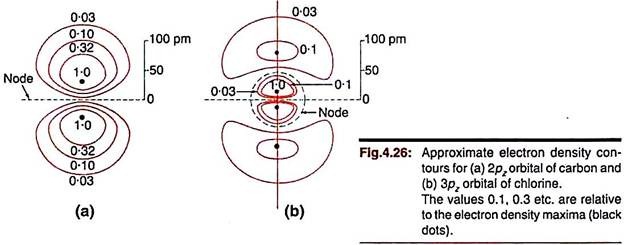
Contour diagrams are obtained by joining points at which Ψ or Ψ ² has the same value. The construction of the contour diagram for Ψ_1s is illustrated in Fig. 4.25. In three dimensions, these will correspond to concentric spheres. The electron density contours for 2p and 3p orbitals are shown in Fig. 4.26. In three dimensions these lines will correspond to cross-sectional view of curved surfaces. Computerised contour diagrams are now commonly used.

The symmetry properties of the orbitals are interesting. In case of s- and d-orbitals, the wave functions have the same sign at the same distance in opposite directions from the centre of symmetry. These orbitals are thus centrosymmetric and are said to be gerade (German, even); they are labeled by the letter g. The wave functions for p-orbitals have opposite signs on either side at the same distance from the centre—they change sign on inversion about this centre; they are therefore said to be non-centrosymmetric or ungerade (German, uneven) and labeled by u.

Orbits Versus Orbitals:

In the Rutherford-Bohr atom model, orbits represent discrete trajectories of electrons around the nucleus. The behaviour of an electron in such quantized orbits can be described by the laws of Newtonian mechanics applied to an electron as a particle.

The position, momentum and hence the energy of an electron in such orbits may be expressed simultaneously with any degree of precision. Although the idea of orbits could explain the gross features observed in spectra of atoms and related behaviour like ionization energy etc., the concept was found inadequate when wave-particle dualism was established in the behaviour of the electron and the uncertainty principle followed as a necessary consequence.

The idea of orbitals gets introduced in the wave mechanical atom model. The extranuclear part of the atom is supposed to be subject to the fundamental wave equation of Schrodinger framed to suit material particles.

The equation correlates the energy of a system with a function (Ψ) of the space coordinates of a point at some instant of time. Ψ is the amplitude analogue of general wave motion in physics; Ψ²dν gives the probability of finding an electron in the volume element dν at some time. Each physically meaningful solution of the equation is now termed an orbital; they are specified in terms of four quantum numbers—three from the time-independent Schrodinger equation.

The orbitals thus correspond to a description of the probability of finding an electron in various regions in space in an atom. Probably this is the source of the popular misconception often accumulated from the school days – orbits are two-dimensional while orbitals are three- dimensional. In fact, orbitals are abstract mathematical functions having little physical significance except the energy level or state specified by each.

Each orbital has a definite energy value expressed in terms of certain quantum numbers. The energy expressions happen to be the same as those arrived at by Bohr for hydrogen like species. The maximum in the radial density function of the 1s orbital of a hydrogen atom also coincides with the radius of the first Bohr orbit.

But there always exists a basic difference in approach. If we recall the example of a particle in a box treated by the wave equation, we find that there may be nodes where the probability of finding the particle is zero. Yet there may be regions on either side of these nodes where such probability is high. Similar description for electron does not have any parallel interpretation in terms of orbits where the electron is treated exclusively as a particle.

The question – “how can an electron simultaneously exist on both sides of a point through which it never passes” has no sense when we deal with its orbital description. This is merely one of many examples of novel situations arising from the application of quantum mechanics. A similar situation will be found in the idea of “tunnelling”.

4. Many Electron Atoms:

The Schrodinger wave equation becomes increasingly complex as the number of electrons in an atom increases. Several approximations have been proposed to overcome the situation. An early attempt to such approximation by Hartree (1928) and later by Fock and Slater, (1930) starts with one-electron hydrogenic wave functions for each electron ignoring inter-electron repulsion.

The potential energy function for any one electron is obtained by assuming a spherical distribution of the charges of all other electrons. One thus gets a first approximation function for that particular electron. This function is now used to improve the potential energy function for the second electron, resulting in an improved wave function for this one. The process is continued for all n electrons in the system and then again recycled from electron 1 until results of two successive stages do not show any gross variation. The n one-electron wave functions are now said to be self-consistent and their product gives the self-consistent field (SCF) wave function for the system. Inclusion of spin and symmetry criterion (The Pauli exclusion principle) gives the further improved Hartree-Fock wave function (HFSCF).

The effect of inter-electron repulsion on the energy of a multi-electron system may be conveniently tackled in terms of a fractional reduction of the net attraction exerted by the nuclear positive charge on an electron in the neighbourhood of every other electron. This modified nuclear charge is called the effective nuclear charge.