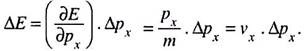Term Paper on Uncertainty Principle | Atoms | Chemistry

In this term paper we will discuss about the uncertainty principle used for determining the position of a particle.

For large or macroscopic objects in motion, the exact position and velocity at any instant of time can be expressed by the laws of Newtonian mechanics. But for a very small (submicroscopic) object like the electron, involvement of the wave character does no more permit the application of Newtonian mechanics. We shall first try to appreciate this point by considering a hypothetical situation.

A “thought” Experiment:

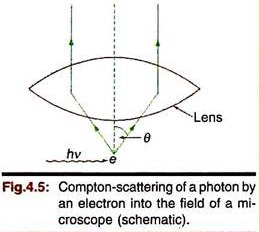
Suppose an imaginary microscope of high resolving power is designed to measure the position and momentum of an electron simultaneously. The resolving power of a microscope may be expressed in terms of the distance Δx between two points which can just be resolved by the microscope. Δx is approximately given by –

Δx ≃ λ/2 sin θ

Where λ is the wavelength of the light used to illuminate the object and θ is the half angle of the lens used (Fig. 4.5.) Clearly, the position of the electron cannot be measured more precisely than Δx – so the minimum uncertainty in the position of an electron in this experiment will be Δx. If we want to keep Δx as small as possible, the wavelength λ of the light used should be as small as practicable—e.g., x-rays or γ-rays.

Now the process requires that an electron is hit by a photon and the photon is scattered into the field of the microscope. In Compton scattering we learned that in such an interaction the photon transfers a part of its momentum (hν/c) to the electron. The exact change in the momentum of the electron cannot be determined precisely since the scattered photon can enter the microscope anywhere within the angle θ. The uncertainty in the momentum of the electron, Δp, can be shown to be of the order –

Δp ≃ hν (sin θ/c) = h sin θ/λ.

If we want to keep Δp small, λ should be very large. This will make Δx large that is increase the uncertainty in the measured position of the electron. On the other hand, if we want precision in the position measurement, the small value of λ will result in greater uncertainty in the momentum determination. Combining the expressions of Δx and Δp ―

Δx Δp ≃ h.

Δx and Δp are the minimum uncertainties in respective cases; the actual uncertainty may be greater. So we write ―

Δx Δp ≥ h.

A more rigorous argument gives ―

Δx Δp ≥ (h/4π), or ћ/2 (where ћ = h/2 )

In a three-dimensional system, similar relations hold for each coordinate axis. In cartesian coordinates, the relations may be stated as ―

Δp_x Δx ≥ h/4π

Δp_y Δy ≥ h/4π

Δp_z Δz ≥ h/4π

Δp_x, Δp_y and Δp_z are uncertainties in the components of momentum along respective axes and Δx etc. are corresponding uncertainties in position.

This uncertainty is a direct consequence of wave-particle duality. A moving particle may be considered in terms of a wave group resulting from superposition of a large number of waves. At a given time, the particle may be located anywhere within the group. The narrower the wave group, the more precisely can we locate the position of the particle. But in a narrow wave group we do not have enough waves to measure the wavelength precisely.

Hence the momentum (= h/λ) becomes uncertain. Similarly, in a wide wave group, we can determine the wavelength (hence the momentum) with greater precision but in that case the position becomes more uncertain. Thus, the uncertainty arises as an essential consequence of the wave-particle dualism and not due to any limitation in our measuring device.

From an analysis of the wave-particle dualism of matter, W. Heisenberg (1927) stated – it is not possible to determine simultaneously both the position and the momentum of a body with any arbitrary desired accuracy. In other words, it is impossible to know both the exact position and exact momentum of an object at the same time.

The product of the uncertainty Δx in the position of a body at any instant and the uncertainty Δp in the x-component of its momentum at the same instant will be at least of the order of h, the Planck constant (precisely h/4). Mathematically stated ―

Δx Δp > h/4π.

[In a three-dimensional system, equivalent expressions apply to other coordinate axis.]

Uncertainties in Energy and Time:

The uncertainty relation holds between any two conjugate properties like energy and time. An alternative expression for the uncertainty principle may be arrived at from the consideration of energy measurement of a particle. We might wish to measure the energy E emitted sometime during the time interval Δt in an atomic process. Here the uncertainty in the time is Δt; this will introduce an uncertainty ΔE in the energy measurement according to the relation –

ΔE Δt > h/4π

This uncertainty relation is also applicable to any time-dependent system. Suppose we wish to measure the energy E of a free particle moving with a velocity ν in the x-direction. The energy E is equal to the kinetic energy of the particle –

If the momentum has an uncertainty Δp_x and the corresponding uncertainty in energy be ΔE, then ―

But velocity v_x = displacement/time = Δx/Δt.

∴ ΔE = Δx/Δt. Δp_x

Or, ΔE Δt = Δx Δp_x

Since the right hand side is > h/4, ΔE Δt > h/4π.

Thus, the product of the uncertainty in energy and the uncertainty in time at which a particle passes over any point is equal to or greater than h/4π.

Position and momentum or energy and time are two pairs of canonically conjugate variables. In classical mechanics, the dynamical situation of a particle is completely defined by any pair of these variables. The physical quantities in each pair are complementary to one another; they are precisely known at the same time in classical mechanics. The prominent involvement of wave nature for microscopic particles now puts a limit to this precision in the form of the uncertainty principle. We are thus led to the development of a new mechanics, called the quantum mechanics.